산술평균 기하평균 포스팅은 일반적인 개요에 대하여 알아보고,
기하평균을 통해 파생되는 원리인 캘리 공식에 대해서도 따로 포스팅 될 예정입니다.
개 요
가끔 주식투자 관련하여 홍보글들을 자주 접할 수가 있습니다.
전문가 연 수익률 70% 많게는 자산을 두배 불렸다고 하면서 광고 하시는 것을 볼 수 가 있고, 펀드 또한 마찬가지죠.
우리가보는 유사투자자문, sns를 통한 전문가들의 리딩광고 등이 대부분 계산이 쉬운 산술평균으로 계산되어져있습니다.
이 부분에 대해서 좀 자세히 파헤쳐 보도록 하겠습니다.
어느 전문가 또는 펀드의 광고를 한번 살펴봅시다.
2018년 ~ 2019년 연수익률 25% 달성 이라고 합니다.
문의해보니 수익이 2018년에는 100%, 2019년에는 손실이 50% 났으니, 평균값을 구해보면 25%라는 것입니다.
일반적인 평균, 즉 산술 평균으로 계산을 해보면 100 - 50 / 2 = 25% 수익률이 나오기는 합니다.
이 전문가가 100만원을 가지고 투자를 했다고 치면,
100% 수익을 봤기 때문에 200만원 자산을 갖게 되겠지요.
그 다음해에 다시 -50% 손실이 났기 때문에 200*0.5 = 100만원.
결국 2018년도 2019년도 수익률은 0%가 됩니다.
이것은 쉽게 예를 들기위하여 전문가를 예를 든것이고, 대부분의 금융투자회사, 펀드등 이러한 산술평균방식으로 현혹하여 고객유치를 하고 있습니다.
산술,기하평균
일단 산술평균과 기하평균이 무엇인지 간단하게 알아보고 가겠습니다.
1. 산술 기하 평균의 기본적 개념
▶ 산술평균(Arithmetic Mean)

- 평균 성적, 평균 키,몸무게 등 일반적인 평균 값을 구하기 위한 공식 입니다.
- 트레이딩 관점에서 이야기를 하면, 한번에 여러개 종목을 진입하여, 그 순간의 기대수익률을 구하는 것
- 즉, 시간적 개념이 녹아 있지 않음
▶ 기하평균(Geometric Mean)
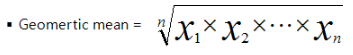
- 기본적인 평균하나로 성장률의 평균을 구할 때 많이 쓰임
- 인구성장률이나 경제성장률을 구할 때 씀
- 시간의 개념이 녹아있어 순차적으로 연속적인 투자 수익률을 계산하기 위함.
2. 왜 기하평균이 중요한것인가? - 변동성 손실
주식 투자 자체가 가격과 시간이 녹아있기 때문에, 우리는 트레이딩을 할 때 시간적 개념을 절대 무시할 수가 없다고 생각합니다. 매일 같이 수익을 내는 데이트레이딩 또한 매일 같이 '시간'을 투자하여 수익을 추구 하기 때문에, 이 기하평균수익률은 중요합니다.
좀 더 자세히 말씀드리면 시간과 가격의 개념이 녹아있는 트레이딩에 여러기간 (Multi - Period) + 하나의 시계열 ( Time Series) 를 이룰 때의 전기간의 평균이라는 것이죠.
예시를 몇가지 들어 보겠습니다.
서두에 예시들었던 전문가 수익률이 18년에는 100% 수익 , 19년도에는 50% 손실이 났다고 하면,
2년간의 산술평균 수익률은 25%
2년간의 기하평균 수익률은 0%가 됩니다.
만약 19년도에 50%가 아닌 60%의 손실이 났다고 하면 어떨까요?
2년간의 산술평균 수익률은 20%
2년간의 기하평균 수익을 계산해보면,
18년도(100%수익) 200만원 -> 19년도(60%손실) 80만원
산술평균으로는 양수의 수익률이 발생하지만, 기하평균으로는 -20%라는 음수 수익률이 나오게 됩니다.
기하평균의 좀 더 자세히 알아보도록 하겠습니다.

1) 변동성이 없는 경우
일단 첫 번째로 10년간 매년 고정(변동성이 없는) 수익,손실 비율이 유지 된다고 하였을 때 데이터를 보도록 하겠습니다.
쉽게 설명드리면 변동성이 없다는 것은 주식 투자가 아닌 은행의 적금의 개념으로 이해하시면 되는데, 고정 수익,손실 비율 -30%~ 30%까지의 구간별 수익비입니다.

매년 고정으로 10%의 수익을 10년간 유지한다고 하였을 때 최고 159.4%의 수익을 달성하게되며,
-10%의 손실을 10년간 유지한다고 하였을 때에는 -56.1%의 손실을 입게 됩니다.
위 데이터를 보면, 변동성이 없이 그대로 상승추세가 유지된다고 하였을 때에는, 계좌 수익이 눈덩이 처럼 늘어나는 것을 볼 수 있는데 이를 "스노우 볼" 효과라고 합니다.
위같은 매매는 돈을 복리로 움직이기 때문에 시간이 지날수록 자산 증가가 기하급수적으로 빨라진다는 것이죠.
복리의
2) 변동성이 있는경우
변동성이 있다는 것은 매년 수익 손실을 반복한다는 것 입니다. 주식투자가 그 대표적인 예가 되겠으며,
매년 손실 수익을 일정비로 반복(변동성 부여) 하는 경우의 데이터를 보도록 하겠습니다.
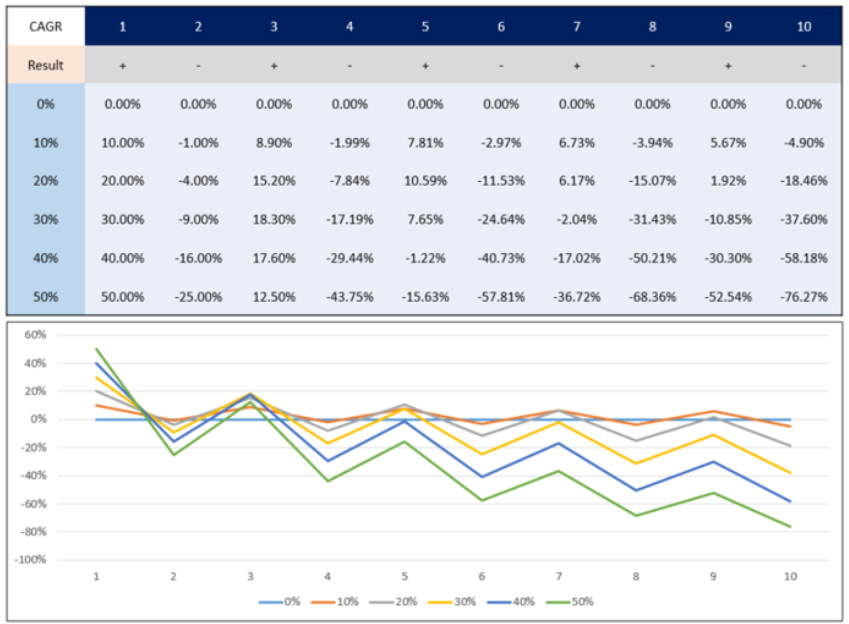
올해는 10% 수익 내년에는 -10% 손실, 이렇게 변동성을 부여하여 계좌를 운영하게 되면, 결론적으로는 계좌는 마이너스를 향해 가게 됩니다. 10% 이상 즉 고 수익으로 가면 갈수록 변동성으로 인하여 손실폭 또한 더욱 커지게 되지요.
이때 생기는 손실을 변동성 손실(Loss from Volatility) 라고 합니다.
결국 같은 수익10%, 손실 10%의 같은 비율로써 투자를 한다하면,
산술평균상으로는 0%의 수익률을 기록하게 되지만, 실질적으로 기하평균으로 따진다면 나의 자산은 마이너스가 되고있는 것입니다.
4. 손익의 비대칭성(P&L Asymmetry)
위에서 변동성이 추가되면 발생하는 손실을 변동성 손실(Loss from Volatility) 라고 하였는데,
이러한 변동성 손실로 인하여 수익과 손실의 편차가 발생하는 것을 손익의 비대칭성(P&L Asymmetry) 이라고 합니다.

이 손익의 비대칭성을 설명을 드리면, 위에서 수익 = 손실이 같은 상태에서 계좌를 운영하게 된다면,
결국 마이너스 그래프를 만들게 되고, 계좌는 손실이 계속 불어나게 됩니다.
이러한 손익의 비대칭성을 극복하기 위해서는 어느정도 수익의 비율이 손실보다 높아야합니다.
그래프를 토대로 설명을 드리면,
| 손실율 | 계산 | 필요 수익률 |
| 1% 손실 | 100/99 = 1.01010.. | 약 1.01 % 수익 필요 |
| 2% 손실 | 100/98 = 1.02040.. | 약 1.02 % 수익 필요 |
| 3% 손실 | 100/97 = 1.03092.. | 약 3.09 % 수익 필요 |
| 4% 손실 | 100/96 = 1.04166.. | 약 4.16 % 수익 필요 |
| 5% 손실 | 100/95 = 1.05263.. | 약 5.26 % 수익 필요 |
| 10% 손실 | 100/90 = 1.11111.. | 약 11.11% 수익 필요 |
| 30% 손실 | 100/70 = 1.42857.. | 약 42.85% 수익 필요 |
| 50% 손실 | 100/50 = 2 | 100% 수익 필요 |
| 90% 손실 | 100/10 = 10 | 900% 수익 필요 |
이러한 손익의 비대칭성을 손실율에 따라서 정리를 하게 되면,
기하 수익률 상 일정비율로 수익>손실 비율로 끌고가야 계좌는 불어난 다는 것을 확인 해볼수 있습니다.
물론 주식에서의 복리 개념은 수익이 보장되어있는 상태에서는 아주 좋은 개념이나,
주식은 개념과는 달리 수익과 손실이 반복되는 변동성이 있는 장입니다.
일단 수익>손실의 경우에도 손익의 비대칭성으로 인하여 해당 오차를 개선하지 않는다면, 결국 자신의 계좌는 기하수익률은 0% 또는 마이너스 수익률을 기록하게 된다는 것이죠
철저한 비중조절과 수익률 높은 매매기준이 필요하다는 결론이 나옵니다.
자 이번에는, 본인의 매매기준이 어느정도 정립이 되었고,
어떤사람이 1억을 3년간 투자, 월 수익률 40%, 손실 30%가 교차된다고 가정을 해보겠습니다.
비중조절없이 계속해서 투자하면 계좌에는 6950만원이라는 결과가 나옵니다.
하지만 이게 월별 수익이 20%의 수익과 10%의 손실이 뒤바뀌게 되면? 3년뒤에는 위와 다르게 4억이 됩니다.
손익률이 30/40 과 20/10 이 다르게 나온다는것인데요.
기하평균의 성질이 결국 '투자비중'을 조절하면 극복이 가능하다는 결론이 나오게됩니다.
위에서 1억투자시에 3년간 월 40/30의 손익비로 운영하게되면 남아있는 돈은 6950만원이라고 말씀드렸습니다.
하지만, 만약 이 투자금 1억에서 40%만 투자비중을 조절해서 운영한다면 어떻게 될까요?
1억 : 40/30비율 = 4천만원 : X(손익비)
X를 구해보게되면 16%의 수익과 12%의 손실이 교차되는 투자 비율로 바뀌게 되었기 때문에,
기하 평균 수익률은 플러스가 되게됩니다.

이 처럼 자신만의 매매기준이 있다면, 투자 비중 조절을 했을 떄
약 40%로 투자하는경우 최고의 기하평균 수익률이 나오게되고, 투자비중이 80%이상 넘어가게되면 다시 기하 평균 수익률은 마이너스를 기록하게 됩니다.
결론은 본인 매매기준의 승률에 따라 투자비중 조절을 잘하면 계좌는 산술평균의 착시 속에서 벗어나 기하 평균 수익률을 통해 계속해서 불어나게 되는 것이죠.
위의 내용에서 파생되는 투자 운용 전략이 섀년의 균형 복원 포트폴리오, 켈리 베팅 전략입니다.
해당 내용에 대해서는 다음 포스팅에서 설명드리도록 할게요.
마무리하며
카톡방에서 제가 이번 한달에 대해서는 포트를 정리하고, 매매전략에 대한 수정을 하겠다고 말씀을 드렸었습니다.
개인적으로 저는 70~80% 이상의 승률을 가진 매매기준을을 갖고서 매매를 하고 있습니다.
하지만 승률이 높은 매매기준도 중요하지만,
매매기준을 활용하는 전략이 더욱 중요하다는 것을 이번에 다시한번 느끼게 되었네요.
다양한 글들을 수집하고, 저 또한 공부를 하면서 저의 매매전략에 대해서 정립을 할 필요성을 느꼈습니다.
여러분도 본인 매매기준의 승률에 대해서 통계를 내어보고, 리스크를 줄여보는 전략 정립을 해보시는건 어떨지요^^
참고자료
1) 메트릭 스튜디오
2) https://0176110001.blog.me/221358152289
'비공개 > 과거' 카테고리의 다른 글
| 삼성전자의 30% 캡률에 대해서 알아보자 (1) | 2020.01.21 |
|---|---|
| 1월 20일 주식시황) 오늘의 상한가 및 주식시세분석 (2) | 2020.01.20 |
| 2020.01.16 꿈개미 관심종목 - 에이비엘바이오(2) (6) | 2020.01.18 |
| 1월 16일 주식시황) 오늘의 상한가 및 주식시세분석 (1) | 2020.01.16 |
| 1월 14일 주식시황) 오늘의 상한가 및 주식시세분석 (8) | 2020.01.14 |




댓글